1)定义
调节阀的流量特性是指介质流过阀门的相对流量与相对开度的关系。数学表达式为:
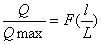
(5—1)
其中:
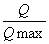
———相对流量(Q———某一开度下的流量)
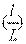
———相对开度,
调节阀阀芯某一位移 ι与全开位移 L 之比。
一般来说,改变调节阀阀芯、阀座间的节流面积,便可以调节流量。由于多种因素的影响,改变节流面积,流量改变,导致系统中所有阻力的改变,使调节阀前后压差改变,为了便于分析先假定阀门前后压差不变,然后再引伸到真实情况进行讨论。前者称为理想流量特性,后者称为工作流量特性。理想特性又称固有流量特性。理想特性主要有直线、对数两种。
1) 直线特性
直线特性是指调节阀的相对流量与相对开度成直线关系,即单位行程变化引起的流量变化是常数,用数学式表达为:
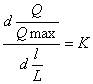
(5—2)
式中:K—常数,即为调节阀的放大系数。
将上式积分得:
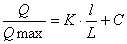
式中:C—积分常数。
代入边界条件: ι=0时,Q=Qmin,ι=L时,Q=Qmax,从积分式中解出常数项为:
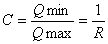
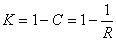
得
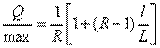
上式表明,Q/Qmax与ι/L之间呈直线关系,在直角座标上得到一条直线。因R=30,当ι /L时,Q/Qmax=1/R =0.033;当 ι/L=1,即全开时Q/Qmax=1。连接上述两点得直线特性曲线,见图5-1之1。从图中看出直线特性调节阀的曲线斜率是常数,即放大系数是一常数。
从公式中看出,当开度 ι/L变化10%时,所引起的相对流量的增量总是9.67%,但相对流量的变化量却不同。我们以开度10%、50%、80%三点为例,其相对的流量见表5-4,则:
在10%开度时,流量相对变化值为:
可见,直线特性的阀门在小开度工作时,流量相对变化太大,调节作用太强,易产生超调引起振荡;而在大开度时,流量相对变化小,调节太弱,不够及时。为解决上述问题,希望在任意开度下的流量相对变化不变,产生了对数特性。
3)对数(又称等百分比)特性
表5-4 流量特性的相对开度和对应流量(R=30)
相对流量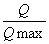 % \ 相对开度 % \ 相对开度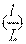 % % |
0
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
|
直线流量特性
|
3.3
|
13.0
|
22.7
|
32.3
|
42.0
|
51.7
|
61.3
|
71.0
|
80.6
|
90.3
|
100
|
|
等百分比流量特性
|
3.3
|
4.67
|
6.58
|
9.26
|
13.0
|
18.3
|
25.6
|
36.2
|
50.8
|
71.2
|
100
|
|
快开流量特性
|
3.3
|
21.7
|
38.1
|
52.6
|
65.2
|
75.8
|
84.5
|
91.3
|
96.13
|
99.03
|
100
|
|
抛物线流量特性
|
3.3
|
7.3
|
12
|
18
|
26
|
35
|
45
|
57
|
70
|
84
|
100
|
对数特性是指单位行程变化引起相对流量变化与该点的相对流量成正比,即调节阀的放大系数是变化的,它随相对流量的增加而增大。用数学式表达为: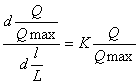
经过积分,同直线特性的推导过程一样,将上式代入边界条件,定常数项,得:
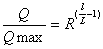
(5-4)
从上式看出,相对开度与相对流量成对数关系,故称对数特性。在直角座标中,得出一条对数曲线,见图5-1之2。
为了和直线特性比较,同样以开度10%、50%和80%三点为例,当开度变化10%时,从表1-4中得出:
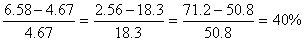
可见,它单位位移变化引起的流量变化与此点的原有流量成正比,而流量相对变化的百分比总是相等的,故又称等百分比特性。